18 de October, 2016

Columna: Las catástrofes del transporte santiaguino

Hasta 1979 el cumplimiento de las normas de estacionamiento en el centro de Londres se mantenía dentro de rangos normales en cuanto a pago de parquímetros y escaso uso de lugares no permitidos para estacionar. Todo cambió, repentinamente, en 1980, cuando de la noche a la mañana el número de vehículos estacionados ilegalmente aumentó un 40% y se produjo un significativo incremento en el número de conductores que, estacionados en sitios con parquímetros, simplemente no pagaban. La sorpresiva situación del sistema de cumplimiento de reglas en los estacionamientos de Londres fue la materia del estudio de Elliott y Wright (1982) con un enfoque que, aparentemente, no había sido aplicado antes en estudios de comportamiento en transporte, donde se mezclan los incentivos económicos, el contexto social y los valores y principios de cada persona.

Ninguna variable relevante que podía servir para explicar la debacle de los estacionamientos había cambiado ostensiblemente: se había producido una reducción en el número de inspectores designados a fiscalizar el cumplimiento de las reglas, pero fue leve. Por otro lado, la multa por estacionar ilegalmente se había mantenido constante por algunos años y el sistema de cobro de multas no había cambiado. Es decir, si había cambios en las variables que se espera afectan la decisión de no cumplir con la norma, estos cambios se habían producido gradualmente en el tiempo (por ejemplo, la reducción paulatina del valor real de la multa por inflación). Entonces, Elliott y Wright sacan de debajo de la manga la teoría de catástrofes para explicar el colapso de los estacionamientos londinenses. En breve, la teoría de catástrofes (debida al matemático francés René Thom) trata de explicar el cambio abrupto en el comportamiento de un sistema, que se produce por cambios menores (o poco perceptibles) en las circunstancias que condicionan el estado de tal sistema.

Si se define el esfuerzo de fiscalización como el número de inspectores de estacionamiento multiplicado por la multa que se cobra en caso de no cumplir con las reglas, se espera que a mayor esfuerzo de fiscalización, menor es el porcentaje de gente que se estaciona ilegalmente, pues el incentivo a no pagar depende del nivel de fiscalización por un lado, y del valor de la multa por otro. Es decir, uno esperaría que la relación entre el esfuerzo de fiscalización y el nivel de estacionamiento ilegal luzca más o menos así:

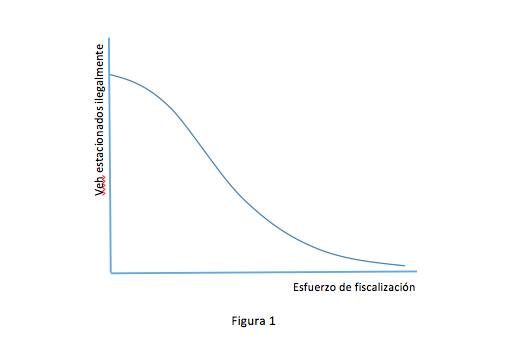
Razonable, ¿cierto? Sin embargo, lo que Elliott y Wright proponen es que tal relación es en realidad así:

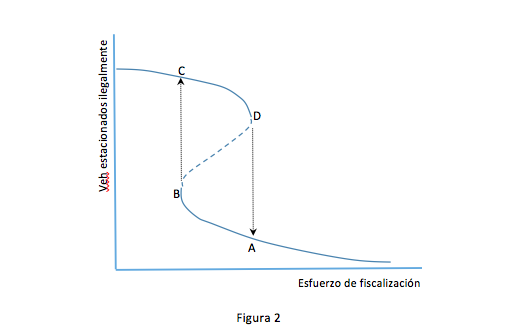
En la Figura 2, el estado A es lo que podríamos llamar “normal”: dado un esfuerzo de fiscalización razonable, el nivel de no cumplimiento por parte de los usuarios es bajo. Luego, si se produce un deterioro leve pero paulatino del esfuerzo de fiscalización (por menor número de fiscalizadores, menor multa, no pago de multa o combinación de todas) el sistema lentamente se mueve al punto B. Lo que caracteriza al modelo de catástrofe es que el punto B es inestable y de él se puede pasar rápidamente al punto C: para un mismo esfuerzo de fiscalización aumenta abruptamente el número de infractores. Los fiscalizadores ahora están sobrepasados. En palabras de Elliott y Wright, el sistema “colapsó”. Se produjo la catástrofe.

La explicación de tal catástrofe se basa en un espiral de deterioro. Un aumento en el número de infractores para un número de inspectores fijo, hace que éstos tengan que cursar más multas, pero el tiempo que les toma multar es mucho mayor que el tiempo que necesitan para inspeccionar un vehículo que está estacionado legalmente. Es decir, la tasa de inspección real disminuye con el número de infractores. Luego, al haber una menor tasa de inspección, los conductores se dan cuenta de la menor probabilidad de ser pillados infraccionando y más usuarios deciden no pagar parquímetro o estacionar ilegalmente. Luego, la tasa de inspección real disminuye aún más y así sucesivamente, en un espiral que puede escalar explosivamente. Dicho de otra forma, cuando hay un alto número de infractores, el incentivo a que un no infractor se transforme en infractor es mucho mayor porque la probabilidad de que lo descubran, entre un mar de infractores, es menor.

Elliott y Wright no pueden demostrar, en un sentido matemático, que en Londres aplica un modelo de catástrofe como el de la Figura 2. Más bien proponen el modelo de catástrofe como una hipótesis que se ajusta de forma satisfactoria a la observación empírica del rápido aumento en el no cumplimiento de las reglas de estacionamiento. De hecho, un resultado similar al observado en Londres puede producirse con una curva como la de la Figura 1, que tenga una pendiente muy empinada en su sección central.

¿Existen “catástrofes” similares a la de los estacionamientos de Londres en el transporte de Santiago hoy?

La candidata número 1 es la evasión en Transantiago (o el robo en Transantiago), actualmente estimada en un 30%, totalmente fuera de rango cuando se compara con los niveles de evasión en sistemas de transporte público con niveles de formalización comparables a Transantiago (Tirachini y Quiroz, 2016). Hay al menos un aspecto en que el caso de la evasión de Transantiago es análogo al de los estacionamientos de Londres de los años 70-80: como la evasión está “desmadrada” es menos probable que a un evasor lo descubran hoy que cuando la evasión era, digamos, 18%. Con el nivel actual de evasión, en un bus fiscalizado es más probable que a un evasor no lo descubran a que lo descubran. Además, al haber más evasores, los inspectores fiscalizan menos gente en su jornada de trabajo pues el proceso de infraccionar a un pasajero es lento y se hace con carabineros. Sin embargo, a diferencia del caso descrito en Londres, el aumento en la evasión en Transantiago ha sido más o menos sostenido en los últimos 3 años y no se puede identificar un aumento abrupto en la evasión en relación a períodos anteriores.

Otro caso es el de los vendedores, cantantes y músicos con parlantes estridentes (y hasta predicadores) que invadieron los trenes del Metro de Santiago. La invasión, que se consumó en cosa de meses, se parece más al caso de Londres en la velocidad con que se produjo el colapso. Es improbable que Metro haya reducido su contingente de inspectores en la red (el único desincentivo que tienen los infractores), sin embargo, de la noche a la mañana pasamos de un estado de viajes tranquilos, que caracterizó al Metro de Santiago desde su fundación, a la, a veces, insufrible situación actual.

¿Qué hacer para devolver un sistema “colapsado” a un estado “normal”? El modelo de catástrofe indicaría que se requiere un esfuerzo de inspección significativo (en la Figura 2, pasar del punto C al D), para tener alguna posibilidad de volver a una situación normalizada, es decir, un salto del punto D al punto A. Una vez que se llega al punto A, el esfuerzo de inspección se puede relajar hasta cierto punto sin llegar a un umbral inestable, como es el punto B. Esto coincide con la recomendación de Tirachini y Quiroz (2016) para reducir la evasión en Transantiago, quienes señalan que en la situación actual se requiere un esfuerzo mayor de fiscalización (posiblemente aumentar la fiscalización en un orden de magnitud) para devolver el sistema a un estado tolerable y sostenible de evasión, luego de lo cual se puede tener un nivel de fiscalización más bajo, en estado de régimen. Elliott y Wright sugieren un atajo, que es concentrar primero los fiscalizadores en aquellas áreas con mayor nivel de infracción, y una vez que se pasa de colapso a normalidad localmente, derivar el exceso de fiscalizadores a las demás áreas. Pero notar que esto solo tiene sentido si, en régimen, se puede tener un esfuerzo de inspección global que haga que el sistema se mueva alrededor del punto A y no alrededor del punto B.

Si bien la evolución de la evasión en Transantiago no puede llamarse una catástrofe en el sentido matemático (aumento abrupto en poco tiempo), el resultado es el mismo al de Londres: un sistema “colapsado” en el cumplimiento de una regla, pudiendo llegar a una catástrofe financiera de no mediar un cambio estructural en cómo se enfrenta el problema. Una condición necesaria para tratar de devolver un sistema colapsado a situaciones de normalidad es incrementar significativamente el esfuerzo de fiscalización, lo que en el caso de Transantiago requiere un cambio radical en cómo se ha abordado el problema, dentro de un paquete multidimensional de medidas antievasión. Las autoridades tienen la última palabra.

Agradecimiento: a Jaime Gibson, profesor de la Universidad de Chile, quien en una discusión sobre evasión en Transantiago me sugirió leer el artículo de Elliott y Wright.

Referencias

Elliott, J.R., Wright, C.C. (1982) The collapse of parking enforcement in large towns: some causes and solutions. Traffic Engineering and Control,23(6):304–310

Tirachini, A., Quiroz, M. (2016) Evasión del pago en transporte público: evidencia internacional y lecciones para Santiago. Documento de Trabajo, Departamento de Ingeniería Civil, Universidad de Chile, Julio de 2016. Disponible en https://www.camara.cl/pdf.aspx?prmTIPO=DOCUMENTOCOMUNICACIONCUENTA&prmID=15696

Ver también:

Tirachini, A. (2016) Transantiago: ¿Cómo reducir la evasión? Diagnóstico y propuesta de paquete de medidas. Seminario ISCI, presentación disponible en http://www.isci.cl/wp-content/uploads/2016_08_evasion.pdf

Opinión

Por Alejandro Tirachini Hernández

Académico de la División de Ingeniería de Transporte del Departamento de Ingeniería Civil de la Universidad de Chile.

Ingeniero Civil y Magíster en Ingeniería de Transporte (U. de Chile), PhD (U. of Sydney). Ha trabajado en proyectos de investigación en transporte en Chile, Australia, Singapur y Alemania, y como consultor y analista de servicios de transporte público en Chile y Australia.

Comentarios de Disqus